Integración por partes

 

La integración por partes es una técnica fundamental en cálculo que se utiliza para integrar el producto de dos funciones. Su base se encuentra en la regla del producto para derivadas, pero se aplica de manera inversa para funciones integradas. La fórmula general es:

                                                       ∫udv=uv−∫vdu

Donde:

-u es una función diferenciable.

-dv es una función integrable.

-du es la derivada de u.

-v es la integral de dv.

El método se basa en seleccionar adecuadamente u y dv para simplificar la integral original y facilitar su evaluación.

Identificación de u y dv:

Para aplicar la integración por partes, seleccionamos u y dv de la función original ∫udv. Una regla mnemotécnica útil es utilizar "LIATE":

Logarítmicas (ln(x)): =u=ln(x) o u=ln(ax) si hay un término logarítmico.

Inversas (1/x): =1u=x1​ si hay un término inverso.

Algebraicas (polinomios): u como un polinomio si la función contiene términos algebraicos.

Trigonometric:

u=sin(x) o =cos u=cos(x) para funciones trigonométricas.

u=ex para funciones exponenciales.

Exponenciales:

u=ex para funciones exponenciales.

Al seleccionar u y dv siguiendo esta guía, buscamos simplificar la integral original y hacer más manejable la derivada de u o la integral de dv.

Fórmula de Integración por Partes:

La fórmula de integración por partes se deriva de la regla del producto para derivadas y se expresa como:

∫udv=uv−∫vdu

Esta fórmula permite expresar una integral complicada como el producto de dos funciones menos la integral de otro término. Es esencial recordar que este proceso puede requerir repetición para llegar a una expresión más fácil de integrar.

EJEMPLO:













                                                        

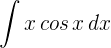
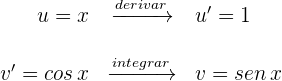
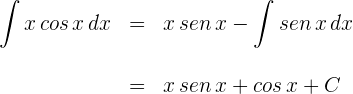
                                                         https://youtu.be/93kW5colCAU

Comentarios

Publicar un comentario

Entradas más populares de este blog

Algebra de conjuntos

Imagen
  El álgebra de conjuntos forma parte de lo que conocemos como teoría de conjuntos,  que un conjunto es la agrupación de elementos de distinta índole, como pueden ser letras, números, símbolos, funciones, figuras geométricas, entre otros. Lo aprendido en clase: Fue que pudimos diferenciar o observar las intersecciones de lo que ya se había visto anterior mente y nos ayudo a poder reforzar el tema  OPERACIONES CON CONJUNTOS  Unión : La unión de dos o más conjuntos contiene todos los elementos que pertenezcan, al menos, a uno de dichos conjuntos. Se indica con la letra U. Ejemplo: A={9,34,57,6,9} B={10,41,57,9,16} AUB={9,34,57,6,9,10,41,16} Intersección:  La intersección de dos o más conjuntos incluye los elementos que comparten dichos conjuntos. Se indica con la U invertida(∩).  Ejemplo: A={a,r,t,i,c,o} B={i,n,d,i,c,o}       A∩B={i,c,o} Diferencia:  La diferencia de un conjunto respecto a otro es a igual a los elementos del pri...
Leer más

Calculo de volúmenes "Método de discos y arandelas"

Imagen
Método de  discos Si una región del plano, se hace girar al rededor de un eje paralelo al eje  , de tal forma que se genera un sólido de revolución cuyas secciones transversales perpendiculares al eje de rotación, son discos con centro en el eje de revolución.  Entonces el volumen del sólido esta dado por donde   es el radio del disco expresado en términos de la variable de integración. Ejemplos: https://youtu.be/58-urgd6GJU?si=C4D7N5WhacafZzl1 Método de Arandelas Este método se basa en el método anterior llamado “Método de Discos” pero en este caso se usa dos discos.  El disco mas pequeño es una vacuna por la que se le da el nombre de una arista por formar una especie de solido hueco.  En términos generales, este método se utiliza cuando el eje de rotación se encuentra a una distancia de la función que formara el solido.  Este espacio entre el eje y la función crea un hueco en el solido, por esto mismo se necesita restar el área del hueco al soli...
Leer más

Espacio muestral y evento - probabilidad

Imagen
En teoría de probabilidad, el espacio muestral y los eventos son conceptos fundamentales que se utilizan para describir y analizar experimentos aleatorios. Aquí te explico cada uno de estos conceptos: Espacio Muestral: El espacio muestral, denotado comúnmente como Ω (omega), es el conjunto de todos los posibles resultados de un experimento aleatorio. Cada elemento del espacio muestral representa un posible resultado del experimento. El espacio muestral puede ser finito o infinito, según el contexto del experimento. Por ejemplo, si lanzas un dado, el espacio muestral es {1, 2, 3, 4, 5, 6}, que es finito. En un experimento como el lanzamiento de una moneda hasta que salga cara, el espacio muestral es infinito: {cara, cara, cara, ...}. Evento: Un evento es un subconjunto del espacio muestral. Representa un conjunto de resultados que pueden ocurrir en un experimento aleatorio. Los eventos pueden ser simples o compuestos. Un evento simple contiene un solo resultado, mientras qu...
Leer más